Normál / Gaussian eloszlás:

TLDR:

Egy függvény/görbe ami segít kiszámítani egy esemény vagy állapot valószínűségét abban az esetben ha az esemény/állapot valószínűsége egy bizonyos érték körül található és az adott értéktől távolodva fokozatosan kisebb esély van az esemény/állapot bekövetkezésére.

Példa:

Ha júliusban 1-jén a hőmérséklet az elmúlt évek mérése alapján 30 fok, akkor a következő évben a legvalószínűbb, hogy július 1-jén a hőmérséklet ismét 30 fok lesz. Ez azonban nem biztos, csak a legvalószínűbb, lehet, hogy csak 27 fok, de lehet hogy 35. Az utóbbi 2 érték azonban kevésbé valószínű mint a 30. Akkor lesz a hőmérsékletet leíró görbe normál eloszlású, ha a 30 foktól mind balra, mind jobbra ugyanolyan intenzitással csökken a hőmérséklet értékek valószínűsége. Ebben az esetben ugyanolyan valószínűséggel lehet 20 fok mint 40 fok.

Kissé beleásva magunkat:

Szokás még haranggörbének, Gauss-görbének hívni. Legfontosabb paraméterei a μ (mű) mely a várható értékét adja meg az eloszlásnak, illetve a σ (szigma) mely négyzetre emelve megadja az eloszlás varianciáját azaz azt, hogy az eloszlásunk mennyire hajlamos "szétkenődni", mennyire szóródnak szét benne az értékek. A σ-t általában szórásnak (angolul standard deviationnek, SD) szokták emlegetni.

Képlete szemet gyönyörködtető:

 

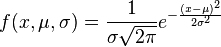
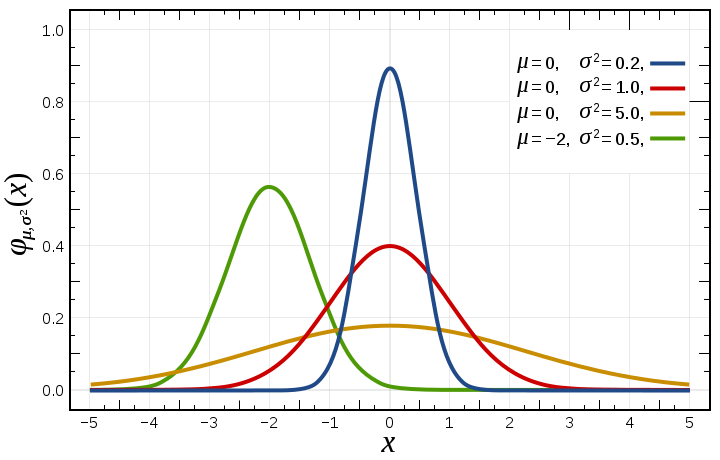A képen különböző normál eloszlás görbék látszanak, feltüntetve a hozzájuk tartozó paraméterekkel. Látható, hogy a μ határozza meg esetünkben a görbénk közepét ahol a legjobban csúcsosodik. A σ² érték minél nagyobb, annál jobban terpeszkedik a görbénk, minél kisebb, annál jobban ágaskodik (oh!). Fontos megjegyezni, hogy a görbe alatti terület összege mindig 1. A normál eloszlás egy speciális formája a standard normál eloszlás, aminek a várható értéke 0, szórása 1 (képen pirossal jelölve)

A normális eloszlás egy alapvető függvény a tudományok világában, szinte minden szakterületen használják (gazdaságtan, szociológia, alkalmazott tudományok, stb) mivel sokszor kiválóan tudja modellezni a valóságot, noha tökéletes formában nem nagyon lehet fellelni, nem fogunk olyan mintát találni ami tökéletesen illeszkedik egy normál eloszlás függvényre. 

A σ fontos érték egy normál eloszlás görbénél, ezzel lehet felosztani a görbét ember számára is könnyen megjegyezhető részekre. Annak a valószínűsége, hogy az esemény/állapot várható értéktől (μ) 1σ távolságon belüli értéket vesz fel 68%, 2σ távolságon belüli értékekre 95%, míg 3σ távolságon belüli értékekre 99%.

Az y tengelyt megvizsgálva joggal tehetjük fel a kérdést: Ha rábökök egy pontra az x tengelyen, akkor az eseményünk y valószínűséggel bekövetkezik? Nem egészen, mivel a görbénk folytonos természetű, ezért a valószínűsége nem az egyenesünk magassága, hanem egy adott terület 2 pont között.
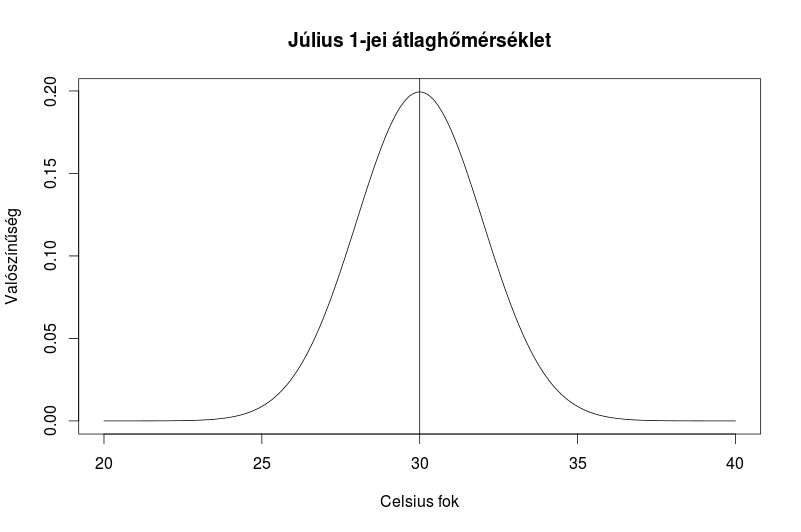
Hogy sikerüljön értelmezni, ismét vegyük elő az időjárásos példánkat. Ha megkérdezem, hogy mi a valószínűsége annak, hogy július 1-jén 30 fok lesz, akkor az nem egyenlő a normál eloszlási görbénk várható értékével, hiszen ugyanúgy lehet 30,0001 fok, vagy 29,9999 fok. Gyakorlatilag annak az esélye, hogy pontosan 30 fok legyen újra, szinte 0 az esélye. A képen a vonal jelöli a 30 fokot. A vonalnak kvázi nincs vastagsága, ezért nem beszélhetünk területről.

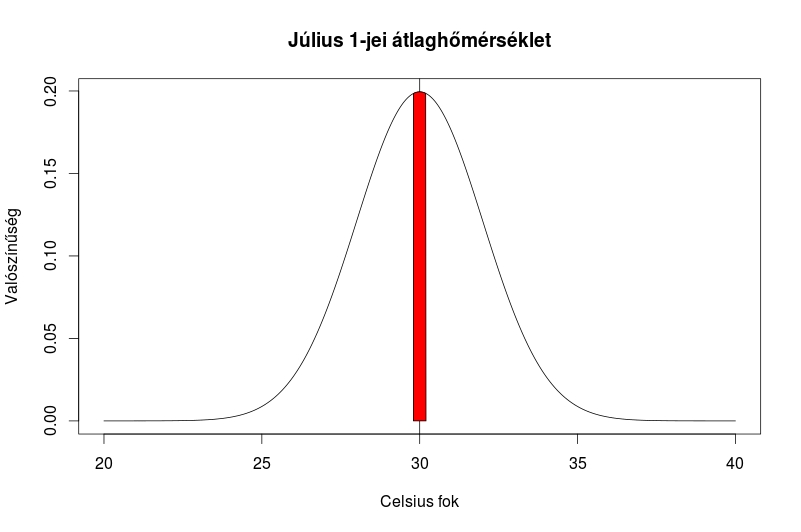
Ellenben ha azt vizsgáljuk, hogy mi a valószínűsége annak, hogy július 1-jén a hőmérséklet 29,8 és 30,2 közé esik (30 +- 0,2), akkor már reális esélyekkel pályázhatunk rá, hogy kiszámítsuk pontosan, mennyi is ennek az esélye. A képen a piros terület jelöli a területet ami lefedi a fent említett intervallumot.

A σ-nál mindenképpen meg kell említeni a z-értéket amely egy előjellel rendelkező érték és azt méltatja jelölni, hogy egy megfigyelt érték standardizálás után hány σ távolságra található a standard normál eloszlási görbe várható értékétől.
-"Mivan?"
Elmagyarázom!

Tegyük fel, hogy Gyuszi hentesnél kapható a legfinomabb szalámi amit ő előre csomagolva, 0,5 kg-os csomagokban árul. Szorgalmas nyugdíjasként felírtad az összes baklövését és tudod, hogy a szalámi tényleges várható súlya 0,45 kg, szórása 0,02 kg. Gyuszi jóindulatú, de azért a szíve mélyén egy kicsit köcsög is. Főleg a nyugdíjasokkal.. Szeretnéd megtudni, hogy mi a valószínűsége annak, hogy csak 0,4 kg-os szalámit kapjál. Ez esetben azt akarod kiszámolni, hogy mi a valószínűsége annak, hogy x<0,4. Ezzel csak annyi a gond, hogy normál esetben ehhez kéne egy táblázat, ami specifikusan erre a várható értékre és erre a szórásra kiszámolja neked, hogy mi a valószínűsége annak, hogy egy random x érték kisebb mint 0,4, azaz 0,4-től balra található görbe alatti területet. Mivel a világ összes normál eloszlás variációja végtelen, ezért ez hiú ábránd marad, azonban megoldás lehet esetleg az, ha csak egy ilyen normál eloszláshoz készítünk egy ilyen táblázatot és minden normál eloszlást ehhez vezetünk vissza. Szerencsére létezik ilyen, ez a standard normál eloszlás.

Minden esetben a meglevő problémát standardizálással tudjuk visszavezetni a fent említett standard normál eloszláshoz. A standardizálás lényege, hogy a megfigyelt értékből kivonjuk a várható értéket és elosztjuk a szórással, ezzel megkapva a z-értéket.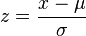 
Esetünkben így alakul a matek: (0,4-0,45) / 0,02 = -2,5
Megnézzük pl ezt az oldalt: http://regentsprep.org/Regents/math/algtrig/ATS7/ZChart.htm
Kiválasztjuk a "Negative z-scores" táblázatból a -2,5-ös számmal kezdődő sort és ebből az utolsó, 0.0 oszlopú cellában levő értéket vesszük alapul, ami 0,0062.
Esetünkben tehát 0,6% az esély arra, hogy 0,4 kilós vagy annál kisebb szalámit adjon nekünk Gyuszi hentes.
R-ben a pnorm függvény megoldja helyettünk az egész procedúrát, de ezt mindjárt magunk is kipróbálhatjuk!

R huszárkodás:

R-ben a főbb eloszlási függvényekhez 4 "jelölés" tartozik, d, p, q, r jelölésekkel. Ezek a következő műveletek rövidítésére szolgálnak:

• d: Sűrűség (Density) --> dnorm(x, mu, sd): Adott x pont(ok)ban mi a normál eloszlású görbénk magassága
• p: Valószínűség (Probability) --> pnorm(x, mu, sd, lower.tail=T): Megadja, hogy egy normál eloszlású görbénken belül definiált véletlenszerű szám a megadott x értéknél mekkora valószínűséggel vesz fel kisebb értéket
• q: Kvantilis (Quantile) --> qnorm(x, mu, sd): Az előző pnorm függvény inverze. x egy 0-1 közötti területet jelöl és a függvény megadja, hogy az x tengelyen hol az a pont, amitől balra pontosan ennyi a területe a haranggörbének.
• r: Véletlenszerű (Random) --> rnorm(n, mu, sd): n darab véletlenszerű számot generál melyeknek az eloszlása normál 

 Maradjunk a júliusi hőmérsékletes példánknál. Először rajzoljuk ki az eloszlást:

mu = 30
sd = 2
# A seq függvény legenerál egy vektort aminek elemei az átadott from-to értékek közötti intervallumot
# veszik fel. Amennyiben a by érték is meg van adva, akkor az értékek közötti differencia pontosan
# ennyi lesz.
# Jelen esetben a kezdő érték 5 SD-vel a mű előtt, a végső érték pedig 5 SD-vel a mű után található,
# a lépésköz pedig 0.01
x = seq(mu-5*sd, mu+5*sd, by=.01)

# Minden egyes x értékhez legeneráljuk a hozzá tartozó magasságot a megadott mu és sd (szigma) értékű
# normál eloszláshoz.
y = dnorm(x, mu, sd)
# Plottoljuk az ábrát, ahol az x tengelyen a legenerált szekvenciánk lesz található, y tengelyen
# a megfelelő x ponthoz tartozó dnormmal legenerált magassága a normál eloszlásnak
plot(x,y, type="l", main="Július 1-jei átlaghőmérséklet", xlab="Celsius fok", ylab="Valószínűség")
# Behúzunk egy cuki vonalat az átlaghoz
abline(v=30)

 Ez legenerálja az első hőmérsékletes képünket

A következőkben eljátszunk a fentebb említett 4 függvénnyel és megnézzük a gyakorlatban is a hasznukat:

1. feladat: Számoljuk ki, hogy pontosan mi az esélye annak, hogy a július 1-jei hőmérséklet értéke 29,8 és 30,2 közé esik

lb = mu - .2
ub = mu + .2

# A következő megadja, hogy hány százaléka esne a véletlenül megválasztott normál eloszlású értékeknek
# a felső érték (30,2) alá
pnorm(ub, mu, sd)
i = x <= ub
polygon(c(x[1], x[i], ub), c(0, y[i], 0), col="red")
# Ezen terület a teljes normál eloszlás 53,9%-a, melyet a piros terület jelül a ploton

# A következő megadja, hogy hány százaléka esne a véletlenül megválasztott normál eloszlású értékeknek
# az alsó érték (29,8) alá
pnorm(lb, mu, sd)
i = x <= lb
polygon(c(x[1], x[i], lb), c(0, y[i], 0), col="green")
# Ezen terület a teljes normál eloszlás 46%-a, melyet a zöld terület jelöl a ploton

# A piros területből még látható rész érdekel minket, melyet úgy kapunk meg, hogy
# a felső határhoz pnorm értékből kivonjuk az alsóhoz tartozó értéket
pnorm(ub, mu, sd) - pnorm(lb, mu, sd)
# Válasz: 7,9% esély van rá, hogy a július 1-jei hőmérséklet 29,8 és 30,2 közé fog esni ismét

2. feladat: Hány szigma (SD) távolságra van az átlagtól az a hőmérséklet ami magasabb a normál eloszlású júliusi várható hőmérséklet értékek 85%-nál? Hány fok ez pontosan?

percentage = .85
zperc = qnorm(percentage)
zperc
# 1.036 SD távolságra van jobbra az átlagtól a 85%-os területet határoló hőmérsékleti pont
# Kis ellenőrzés:
pnorm(mu + sd * zperc, mu, sd)
# A kerekítési hibát leszámítva helyesen gondolkodtunk
degree = mu + sd * zperc
degree
# 32.07 celsius fok az a hőmérséklet ami nagyobb a várható hőmérsékletek 85%-ánál

3. feladat: Generáljon le pár értéket a júliusi hőmérséklet normál eloszlási függvényéből, majd ellenőrizze, hogy a legenerált értékek átlaga és sztenderd eloszlása nagyon hasonló a júliusiéhoz

for (i in 1:5) {
    # A set.seed beállítja a véletlenszám generátornak, hogy a következő számításnál milyen "seedet"
    # használjon. Ez azért kell, hogy a script lefuttatása újra és újra ugyanazt az eredményt adja
    set.seed(i)
    # Legenerálunk 1000 értéket a normál eloszláson belül
    distribution = rnorm(1000, mu, sd)
    cat("\n", i, ". iteráció (")
    cat("Átlag: ",mean(distribution), ", ")
    cat("SD: ", sd(distribution), ")")
}
# Láthatjuk, hogy az átlag 30, az SD 2 körül mozog mindig nagyon kis eltéréssel

A kódot innen tudod letölteni